Customer lifetime period
This is the amount of time that the average customer (or customer segment) remains an active customer with a firm; it is typically measured in years.
When a business has a very stable customer retention rate every year, regardless of the length of loyalty of the customer base or improvements and modifications to customer acquisition and retention – then the calculation of the customer lifetime period is very straightforward using a set formula, which is discussed in this article on calculating the customer lifetime period.
Fluctuating customer retention rates
In business reality, it is unlikely that the retention rate = customer loyalty – will remain constant each year. There are several factors why this is the case, such as:
- Different marketing campaigns and incentives bring in new customers with likely different loyalty patterns over time
- The company itself will try to build and enhance loyalty over time, by improving service or through loyalty incentives
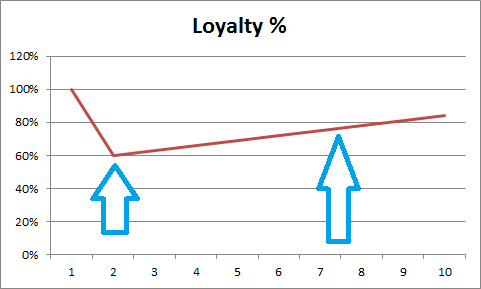
But most importantly, customers who remain loyal for one year or more appear to have a good degree of satisfaction with the firm. In other words, dissatisfied customers are more likely to churn within the early stages of their relationship. The following diagram highlights the most likely pattern of customer loyalty and retention over time for most firms:
As you can see, there is a 60% retention rate from year 1 to year 2, which gradually increases to over 80% over time. This is a relatively typical pattern of customer loyalty to the factors outlined above.
Calculating the customer lifetime period with a increasing retention rate
As there are different retention rates to consider for each year of the customer relationship, we can no longer use the formula (please see the article link above) and we need to do a manual, but simple, calculation.
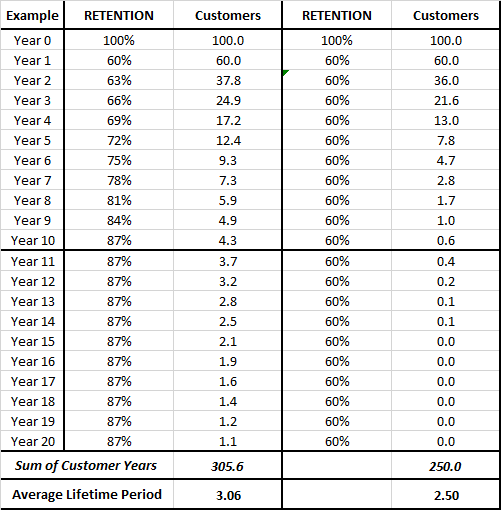
Let’s review the following table:
There is to example shown above. On the left-hand side we have a firm that has increasing retention rate – starting at 60% in the first year, but then increasing progressively to 87% by the end of year 10.
For the simplicity of the calculation, I have assumed that 87% is the maximum retention rate that will be reached. As you can see, by the end of year 20, the firm is only likely to have 1 customer remaining out of 100.
The key calculation occurs in the “customers” column, where we start with a set of 100 customers and then apply the loyalty percentage progressively to work out how many customers we expect to have remaining the following year.
For example, in year one we have a 60% retention = 60 out of 100 customers. In the following year, the retention rate increases to 63%, which means that we will have 63% of the remaining 60 customers = 37.8 customers.
Please note the decimals are used as this is a forecast of likely customers (like a probability measure) – obviously we can’t have 0.8 of the customer.
We continue the calculation down for the full 20 years – or a suitable time period for the business involved, which may be shorter. And then we sum that column of numbers.
In this example, the sum is 305.6 years. This equates to 305.6 total customer years across the 100 customers that we started with. Then we simply divide 305.6 total years by the starting 100 customers, we get an average customer lifetime period of 3.056 (or 3.06 rounded).
The example shown in the other columns on the right, are calculated the same way – except this time with a flat retention rate, to demonstrate that the calculation is correct.
If we have a flat 60% retention rate, then our churn/loss rate is 40% – and using the formula we can determine that the average customer lifetime value period is 2.5 years.
Lifetime period = 1/(1 – retention rate) = 1/(churn rate)
For this example, the lifetime period is 1/0.4 = 2.5 years – which is a match to the above calculated table.